Alice's Challenge —— 梯度泄露

什么是梯度泄露攻击

为了执行攻击，我们首先随机生成一对伪输入和标签，然后执行通常的前向和反向传播。在从伪数据推导出伪梯度后，不像典型训练中那样优化模型权重，而是优化伪输入和标签，以最小化伪梯度和真实梯度之间的距离，通过匹配梯度使虚拟数据接近原始的数据。当整个优化过程完成后，私有的数据（包括样本和标签）就会被恢复。

创建虚假的图片，虚假的标签，送入模型获取虚假的梯度。以虚假的梯度与用户的梯度计算L2损失，更新虚假的图片与虚假的标签。最终虚假的图片和虚假的标签将收敛于十分接近用户原始数据。

该方法有点类似于生成对抗样本的方法，关键在于使用梯度衡量图片与真实图片的距离。

分布式训练

中心式分布训练和去中心化分布式训练

在两种方案中，每个节点首先进行计算，更新其本地权重，然后向其他节点发送梯度。对于中心式训练，梯度首先被聚合，然后返回到每个节点。对于去中心化分布式训练，梯度在相邻节点之间交换

对于前者而言，参数服务器虽然不存储任何训练数据，但是就可以窃取所有参与方的本地训练数据，而对于后者而言，任何参与方都可以窃取与其交互梯度的参与方的训练数据，所以都是不安全的。

形式化

设在每一步 t ，每个节点 i 会从其本地数据集采样一个 minibatch ,来计算梯度

$$\nabla W_{t,i} = \frac{\delta \iota(F(x_{t,i},W_t),y_{t,i})}{\delta W_t}$$

这些梯度会在 N 个服务器上被平均，然后用来更新权重 $W_{t+1} = W_{t}-\eta \overline{\nabla W_t}$

给定从其他参与方 k 获得的梯度 $\nabla W_{t,i}$

我们的目标是窃取参与方k的训练数据! $(x_{t,k},y_{t,k})$

为了从梯度中恢复出数据，我们首先随机初始化一对伪输入x’和标签y‘。然后将其输入模型并获取伪梯度

当我们在优化伪梯度让其接近原始梯度的过程中，伪数据也会逐渐接近原始的真实训练数据。

给定某一步的梯度，我们通过最小化如下目标来获得训练数据

可以用标准的基于梯度的方法进行优化

整个形式化的攻击流程就是这么简单，我们可以来看看示意图

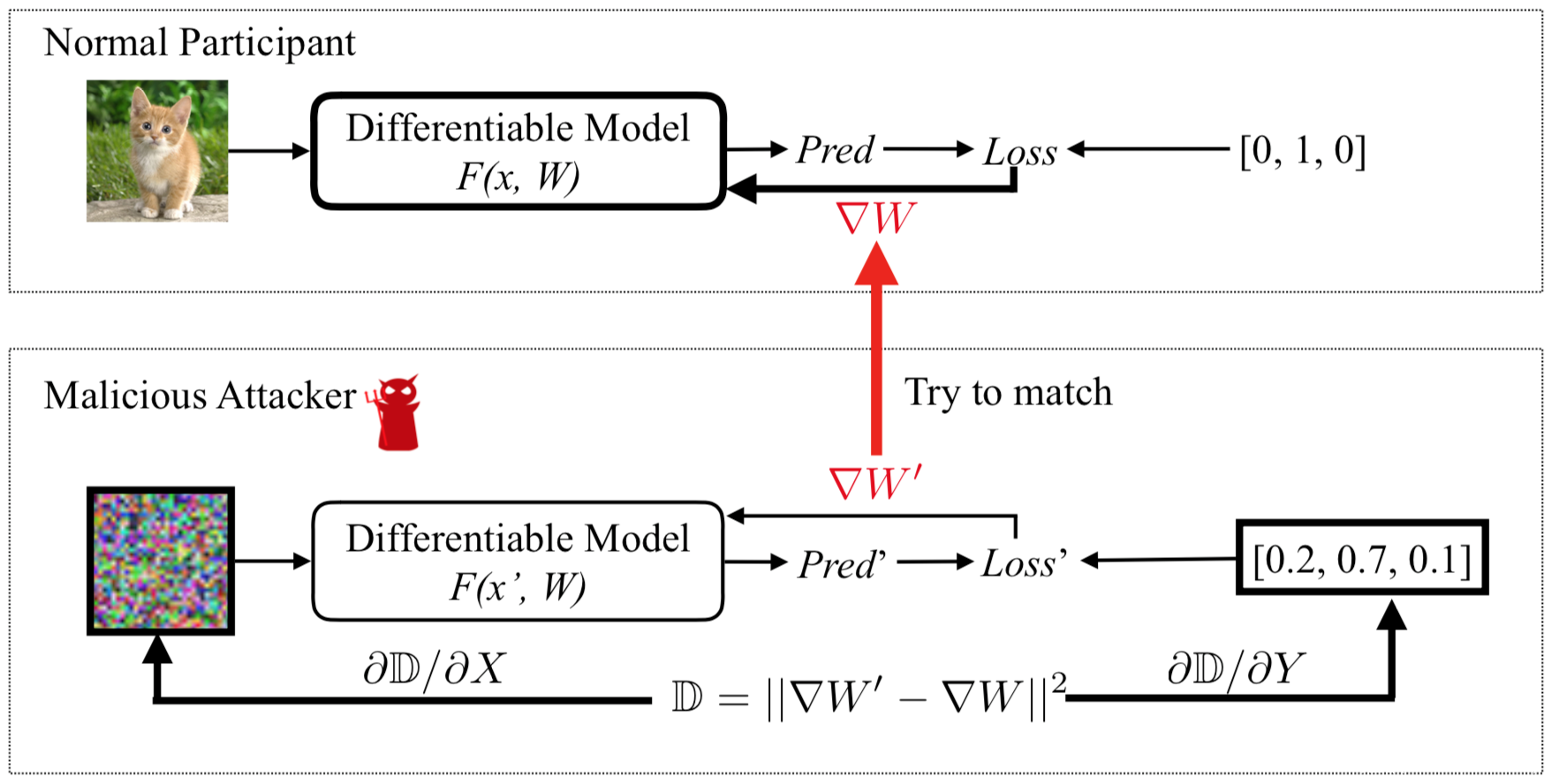
图中，需要更新的变量被粗体边框标记。正常参与方计算∇W，利用其私有训练数据更新参数，攻击者则更新其伪输入和标签，以最小化梯度距离。当优化完成时，攻击者可以从正常参与方那里窃取训练数据。

关于梯度距离与恢复出的图像之间的关系可以看下图

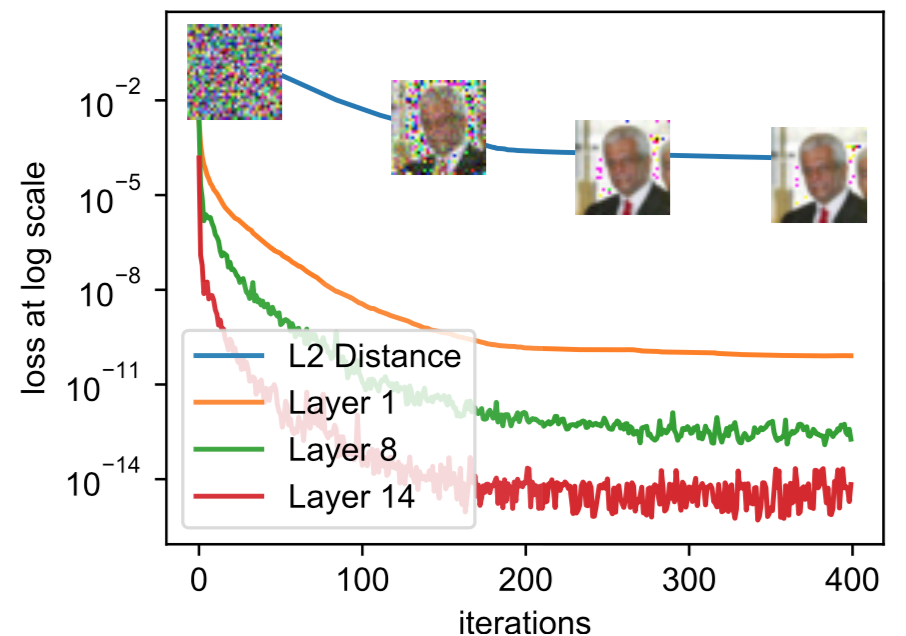
图中，layer -i表示第 i 层真实梯度与伪梯度之间的 MSE(均方误差，预测值与真实值之间的平均偏差的平方)。当梯度距离越小，恢复出的图像与原始图像之间的 MSE 也越小，恢复的效果也就越好。

实战

将标签转为one-hot标签

def label_to_onehot(target, num_classes=100):  
    target = torch.unsqueeze(target, 1)  
    onehot_target = torch.zeros(target.size(0), num_classes, device=target.device)  
    onehot_target.scatter_(1, target, 1)  
    return onehot_target

计算交叉熵

def cross_entropy_for_onehot(pred, target):  
    return torch.mean(torch.sum(- target * torch.nn.functional.log_softmax(pred, dim=1), 1))

权重初始化

def weight_init(m):  
    if hasattr(m, 'weight'):  
        m.weight.data.uniform_(-0.5, 0.5)  
    if hasattr(m, 'bias'):  
        m.bias.data.uniform(-0.5, 0.5)

攻击

# 计算原始梯度        
out = net(gt_data)  
y = criterion(out, gt_onehot_label)  
dy_dx = torch.autograd.grad(y, net.parameters())  
# 与其他参与方共享梯度  
origin_dy_dx = list((_.detach().clone() for _ in dy_dx))

生成伪标签数据

使用torch的randn生成随机数来初始化伪数据，并使用模型对伪数据的预测作为伪标签

dummy_data = torch.randm(gt_data.size()).to(device).requires_grad_(True)  
dummy_label = torch.randn(gt_onehot_label.size()).to(device).requires_grad_(True)  
plt.imshow(tt(dummy_data[0].cpu()))  
plt.title('Dummy Data')  
print('label is %d'%torch.argmax(dummy_label,dim=-1).item())

然后进行训练

optimizer = torch.optim.LBFGS([dummy_data, dummy_label])  
history = []  
for iters in range(300):  
    def closure():  
        optimizer.zero_grad()  
        pred = net(dummy_data)  
        dummy_onehot_label = F.softmax(dummy_label, dim=-1)  
        dummy_loss = criterion(pred, dummy_onehot_label)  
        dummy_dy_dx = torch.autograd.grad(dummy_loss, net.parameters(),create_graph=True)  
        grad_diff = 0  
        grad_count = 0  
        for gx, gy in zip(dummy_dy_dx, original_dy_dx):  
            grad_diff += ((gx - gy) ** 2).sum()  
            grad_count += gx.nelement()  
        grad_diff.backward()  
        return grad_diff  
  
    optimizer.step(closure)  
    if iters % 10 == 0:  
        current_loss = closure()  
        print(iters,"%.4f"%current_loss.item())  
    history.append(tt(dummy_data[0].cpu()))

打印出每次迭代得到的数据

plt.figure(figsize=(12,8))  
for i in range(30):  
    plt.subplot(3,10,i+1)  
    plt.imshow(history[i*10])  
    plt.title("iter=%d"%(i*10))  
    plt.axis('off')  
print("Dummy label is %d"%torch.argmax(dummy_label,dim=-1).item())

法2 共享梯度提取真实标签

正确标签激活的分类损失的梯度在(−1,0)，而其他标签的梯度在(0,1)，正确标签和错误标签的梯度的符号是相反的

# 计算梯度  
out = net(gt_data)  
y = criterion(out, gt_label)  
dy_dx = torch.autograd.grad(y, net.parameters())  
original_dy_dx = list((_.detach().clone() for _ in dy_dx))  
# 生成伪数据及标签  
dummy_data = torch.randn(gt_data.size()).to(my_device).requires_grad_(True)  
dummy_label = torch.randn((gt_label.shape[0],num_classes)).to(my_device).requires_grad_(True)  
optimizer = torch.optim.LBFGS([dummy_data,],lr=lr)  
# 预测真实标签  
label_pred = torch.argmin(torch.sum(original_dy_dx[-2],dim=-1),dim=-1).detach().reshape((1,)).requires_grad_(True)

训练

for iters in range(Iteration):  
    def closure():  
        optimizer.zero_grad()  
        pred = net(dummy_data)  
        dummy_loss = criterion(pred, label_pred)  
        dummy_dy_dx = torch.autograd.grad(dummy_loss, net.parameters(), create_graph=True)  
        grad_diff = 0  
        for gx, gy in zip(dummy_dy_dx, original_dy_dx):  
            grad_diff += ((gx - gy) ** 2).sum()  
        grad_diff.backward()  
        return grad_diff  
  
    optimizer.step(closure)  
    current_loss = closure().item()  
    train_iters.append(iters)  
    train_loss.append(current_loss)  
    mses.append(torch.mean((dummy_data - gt_data) ** 2).item())

防御

我们可以将小幅度的梯度修剪为零。当优化目标被修剪时，这种攻击方案更难匹配梯度。当修剪程度为1% ~ 10%时，对攻击几乎没有影响。当修剪程度增加到20%时，恢复图像上存在明显的伪像。当修剪程度比较大时，恢复的图像不再可识别了，看起来就是噪声，这说明梯度压缩可以成功防止泄漏。

添加噪声 作为防御，也可以在梯度被共享之前，加上噪声。我们使用高斯噪声和拉普拉斯噪声进行实验，其方差范围从$10^1$到$10^4$

防御的效果主要取决于分布方差的大小。当方差为$10^4$时，不能防止泄漏。对于方差为$10^3$的噪声，尽管存在伪影，仍然可以执行泄漏。只有当方差大于$10^2$，且噪声开始影响精度时，恢复出的图像基本不可识别了，方差大于$10^2$的噪声会导致恢复彻底失败。

本题：参照论文源码： https://github.com/mit-han-lab/dlg/blob/master/main.py

exp:

# -*- coding: utf-8 -*-  
  
from PIL import Image  
import matplotlib.pyplot as plt  
  
import torch  
import torch.nn as nn  
import torch.nn.functional as F  
import torchvision  
from torchvision import transforms  
  
print(torch.__version__, torchvision.__version__)  
  
# 定义神经网络  
class AliceNet2(nn.Module):  
    def __init__(self):  
        super(AliceNet2, self).__init__()  
        self.conv = \  
            nn.Sequential(  
                nn.Conv2d(3, 12, 5,2,2),  
                nn.Sigmoid(),  
                nn.Conv2d(12, 12,5,2,2),  
                nn.Sigmoid(),  
                nn.Conv2d(12, 12, 5, 2, 1),  
                nn.Sigmoid(),  
                nn.Conv2d(12, 12, 5, 2, 2),  
                nn.Sigmoid(),  
            )  
        self.fc = nn.Sequential(  
            nn.Linear(768,200)  
        )  
    def forward(self, x):  
        x = self.conv(x)  
        x = x.view(x.size(0), -1)  
        x = self.fc(x)  
        return x  
  
# 定义损失函数  
  
def criterion(pred_y,grand_y):  
    # 交叉熵损失函数  
    tmptensor = torch.mean(  
        torch.sum(  
            - grand_y * F.log_softmax(pred_y,dim=-1),1  
        ))  
    return tmptensor  
  
  
  
# 数据处理 模型加载  
  
ts1 = transforms.Compose([transforms.Resize(32),transforms.CenterCrop(32),transforms.ToTensor()])  
ts2 = transforms.ToPILImage()  
  
  
mydevice = "cpu"  
if torch.cuda.is_available():  
    mydevice = "cuda"  
print("Running on %s" % mydevice)  
  
  
Net = torch.load("Net.model").to(mydevice)  
outpath = 'grad/'  
  
torch.manual_seed(0)  
  
  
# 生成对抗样本  
for i in range(25):  
    original_dy_dx = dy_dx = torch.load(outpath+str(i)+'.tensor')  
    dummy_data = torch.randn(1,3,32,32).to(mydevice).requires_grad_(True)  
    dummy_label = torch.randn(1,200).to(mydevice).requires_grad_(True)  
    optimizer = torch.optim.LBFGS([dummy_data,dummy_label])  
    history = []  
    for iters in range(300):  
        # 优化器迭代 生成对抗样本  
        def closure():  
            optimizer.zero_grad()  
            pred = Net(dummy_data)  
            dummy_onehot_label = F.softmax(dummy_label, dim=-1)  
            dummy_loss = criterion(pred,dummy_onehot_label)  
            dummy_dy_dx = torch.autograd.grad(dummy_loss, Net.parameters(), create_graph=True)  
            grad_diff = 0  
            grad_count = 0  
            for gx, gy in zip(dummy_dy_dx, original_dy_dx):  
                grad_diff += ((gx - gy) ** 2).sum()  
                grad_count += gx.nelement()  
            grad_diff.backward()  
            return grad_diff  
  
        optimizer.step(closure)  
        if iters % 10 == 0:  
            current_loss = closure()  
            print(iters, "%.4f" % current_loss.item())  
        history.append(ts2(dummy_data[0].cpu()))  
  
    plt.figure(figsize=(12, 8))  
    # 可视化对抗样本生成过程  
    for i in range(30):  
        plt.subplot(3, 10, i + 1)  
        plt.imshow(history[i * 10])  
        plt.title("iter=%d" % (i * 10))  
        plt.axis('off')  
    print("Dummy label is %d." % torch.argmax(dummy_label, dim=-1).item())  
    plt.show()